
|
Hands-On-Physics
WAVES
|
Information
|
- Concepts -
|
Equations
One of the main strengths of physics is its use of mathematical modelling.
Waves have speed, and their speed,
like the speed of anything, is just the rate of change of position.
The speed of a wave is distance a wave-crest travels in a second.
v = d÷ t
Waves that vibrate regularly (periodic waves) vibrate from maximum (crest) to minimum
and back to maximum in a uniform time. This time for this one cycle is called the wave period.
During one period (T) a wave crest moves a distance of one wavelength (l).
Considering the wave speed during one cycle, d = L and t = T, so:
v = L÷T
or
v = L x f
Wave timing is sometimes expressed as period (T) which is the time required for one wave-cycle,
but it is often expressed as frequency (f) which is the number of cycles per second.
The unit for frequency is the Hertz, 1 Hz = 1 cycle/sec. Frequency and period are measurements of the same timing, they are reciprocals.
f = 1 / T, T = 1 / f
Wave amplitude describes the shape of the wave. For a water-wave amplitude means height,
for a sound wave it means pressure.
The model for the amplitude of a periodic wave can be written in terms of time or position.
Graphs
a = A sin((2p/T) . t ) , A = maximum amplitude and t = time.
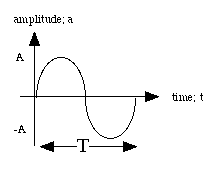
Figure P1
Fixed position
a = A sin((2p/ L) . x) , A = maximum amplitude and x = position.
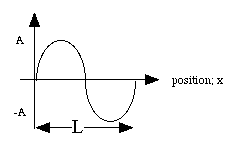
Figure P2
Fixed time (Snapshot)
Previous Page ||
Up a Level ||
Index ||
Next Page