 |
Hands-On-Physics
HEAT & TEMPERATURE
|
Physics
Concepts
|
- Spreadsheets -
|
What to do With Curvy Data
Fitting to a straight line is fine when the data should be straight (linear).
But what about calibrating something like the thermistor that surely is
not linear?
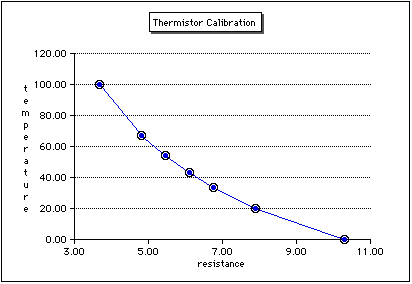
Figure C10a
Non-linear Calibration Curve
Is there an alternative to looking up values on a graph? Is there a mathematical
way of finding the best fit? The answer is yes, providing you know the equation
of the curve. For instance, physics predicts that the resistance of a thermistor
should obey the equation:
R = Ro * a / (T+To) Here, Ro and a are the calibration
constants like a and b in the straight-line fit. To is the ice temperature
in the Kelvin scale, 273.2 °K. Once again, you don't have to understand
the mathematics to use this equation. Here is a AppleWorks spreadsheet
you can use with thermistor data. Just copy it into a AppleWorks spreadsheet
and use it. Enter your calibration data into cells A2...B8. Enter a resistance
reading in k in H1 and read the best fit temperature in °C in cell
H2. The other cells in column H are used to calculate parts of the best-fit
equation. The best-fit for temperatures for plotting the calibration curve
are calculated in cells G2...G8.
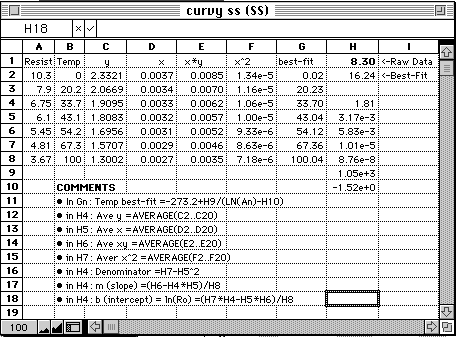
Figure C10b
Curvy Data Spreadsheet
The graph in figure C? shows the best-fit calculations lining up with
the experimental measurements. Suppose the resistance measurements were
not as carefully recorded and looked like this: 10, 7.5, 7.2, 6.1, 5.3,
5, and 3.67 K ohms. Then the calibration curve calculations would then be
quite different than the experimental data.
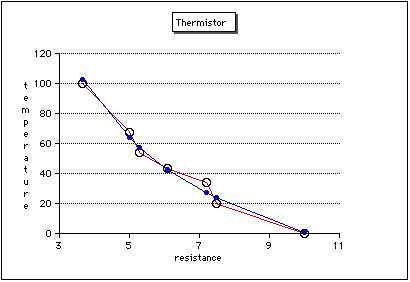
Figure C10c
Curve from Less Accurate Data
Previous Page ||
Up a Level ||
Index ||
Next Page