 |
Hands-On-Physics
MECHANICS
|
Extensions
|
- Force & Changing Speed -
|
The total force pushing the Aircart may be determined by studying its changing
speed. The rate of speed change (acceleration) is directly proportional
to the total force. What is the size of this force? To study the changing
speed of the Aircart, several sequential speed measurements must be made.
You can use a lap-timer stopwatch to time the Aircart
as it moves along the floor, or if Microcomputer-Based-Laboratory apparatus
is available, you can use use MBL to study the
Aircart moving a shorter distance on top of a lab bench.
What's your estimate of the actual force that accelerates the Aircart?
The total force pushing the Aircart may be determined by studying its changing
speed. The rate of speed change (acceleration) is directly proportional
to the total force. What is the force? To study the changing speed of the
Aircart, several sequential speed measurements must be made. You can use
a lap-timer stopwatch to time the Aircart as it moves along the floor, or
if Microcomputer-Based-Laboratory (MBL) apparatus is available, you can
use that to study the Aircart moving a shorter distance on top of a lab
bench.
Measuring Changing Speed with a Stopwatch
If you choose to run the Aircart on the floor, first sweep the floor. Dust
and sand are a problem. If you decide to let distance be the independent
variable, set up a course for the Aircart by marking regular distance intervals
along the floor about half a meter long (masking tape works well). Physicists
measure distance in meters, unless something more convenient shows up. If
you are working on a tile floor, the tiles are probably 1 foot square. If
so, you might want to use feet and convert to meters later ( 1 foot = 0.3048
meters). Run the Aircart over the course you have set up for it, and measure
the time it takes to travel over each interval. From the distances and the
times you can calculate speeds. This is similar to the runner in the Messing
Around experiment.
One problem with the regular distance intervals is that the Aircart crosses
intervals near the end of the course in very short times, too short to measure
accurately. This problem can be solved by using uneven distance intervals
- short in the beginning and longer near the end. We tried a 15 foot long
course, starting with a 1 ft interval and ending with a 5 ft interval. That
approach gave reasonable timing accuracy.
To visualize the changing speed, a speed vs. time graph is helpful. To make
this graph we calculated the mid-times; times when the actual speed would
be the same as the average speed in the interval. The mid-time is half the
time interval added to all the time before ( midtime3 = time1 + time2 +
half time3). We used a spreadsheet, but the calculations and graphing can
be done by hand.

Figure E3
Aircart speed vs. time
After you have set up the course for running the Aircart, make a table
for listing the distances and recording the times for several runs. Run
the Aircart through the course a few times to get several sets of measurements.
Calculate the average time for each distance interval, then calculate the
average speed in each interval. Graph speed vs. time
The slope of this graph is the acceleration of the Aircart. This acceleration
is proportional to the total force on the Aircart. The inertia (mass) of
the Aircart also plays a part and shouldn't be ignored. What's your estimate
of the actual force that accelerates the Aircart?
Measuring Changing Speed with MBL
If you have MBL capability, you can get velocity information about the Aircart
using photogates or a "smart pulley". We had the Aircart pull
a thread attached to a hanging paper clip over a "smart pulley".
The Aircart moved about half a meter along a table top. With our smart pulley
attached to a Vernier Universal Lab Interface (ULI), we used the ULI Timer
to get the speed (velocity) vs. time graph shown below. The speed change
seems quite uniform.
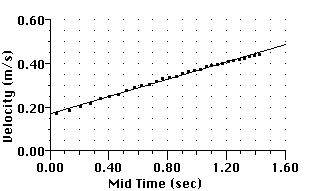
Figure E4
MBL Aircart speed vs. time
The slope of this graph is the acceleration of the Aircart. This acceleration
is proportional to the total force on the Aircart. The inertia (mass) of
the Aircart also plays a part and shouldn't be ignored. What's your estimate
of the actual force that accelerates the Aircart?
Previous Page ||
Up a Level ||
Index ||
Next Page